The eye mask

The circle area is 2πAB/(A+B).

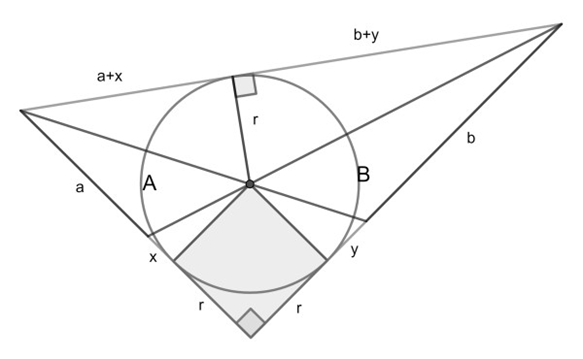
First note that the two triangles both have height r, which is also the circle radius. Name their respective bases a and b. The two small triangles have bases x and y.

From triangle similarity one can show that x/r=r/(b+y) and y/r=r/(a+x). Eliminating r from these two equations leads to x/y=a/b. So we get that b+y=(a+x)b/a=bz/a, where we temporarily named a+x=z. Filling this back in we get that r²=yz=xbz/a.

Now the total area is (r+z)(r+bz/a)/2. By adding up the area of the square and the four right triangles we get that this must be equal to r²+rz+rzb/a. After some algebra, also using the equation for r², we get xb/a+r+rb/a-bz/a=0. Eliminating z, this leads to r=ab/(a+b).

Finally, using A=ar/2 and B=br/2, we reach the desired formula.