Boletín Nº 101
|
|
Boletín del IMI
|
|
1) Palabras del Director
Estimados colegas,
Es un placer informaros de que ya está todo listo para la VI edición del Concurso de Modelización Matemática del IMI (CMM-IMI 2023) que tendrá lugar del 28 de septiembre al 2 de octubre de 2023. Se pueden ver todos los detalles en https://blogs.mat.ucm.es/cmm/
Os recuerdo que, de forma resumida, el CMM-IMI va dirigido a estudiantes universitarios de Grados de Ciencias e Ingenierías a los que se propone modelizar matemáticamente un problema real. El reto no sólo es resolverlo, sino hacerlo en sólo 4 días (del 28 de septiembre al 2 de octubre). Los estudiantes, formando equipos de hasta 3 personas, presentan sus propuestas de solución que es evaluada en primer lugar por un Comité Evaluador formado por profesores de su Universidad y, finalmente, los trabajos seleccionados son reevaluados por un Comité Evaluador Central que elige a los ganadores. El concurso culminará con una ceremonia de entrega de premios que está prevista que se celebre el 15 de noviembre a las 16h en Madrid, en la se que van a repartir cuantiosos premios para los ganadores.
En la presente edición van a poder participar estudiantes de un gran número de universidades de Argentina, Brasil, Chile, España y México.
Os envío un cartel en el que se anuncia el concurso para que, si lo estimáis oportuno, lo difundáis.
Ángel Manuel Ramos
2) Activities from September 21 to 29, 2023
Seminario de Análisis Matemático y Matemática Aplicada
Título: Rearrangement-invariant hulls of function spaces
Orador: Górka Przemysław (Warsaw University of Technology)
Fecha: 21 de septiembre, 2023
Lugar: Aula B07
Hora: 13:00
Organizado por: Departamento de Análisis Matemático y Matemática Aplicada e Instituto de Matemática Interdisciplinar (IMI)
Seminario de Doctorandos
Título: Integrales de Fourier y Conjuntos de Kakeya
Orador: Fernando Ballesta Yagüe
Fecha: 22 de septiembre, 2023
Lugar: Aula 114 y Google Meet
Hora: 17:30
Organizado por: Facultad de Ciencias Matemáticas UCM y Red de Doctorandos UCM, con la colaboración del Instituto de Matemática Interdisciplinar (IMI)
XVII Workshop de Jóvenes Investigadores
Organizadores: Enrique Arrondo (UCM), Pedro D. González (UCM), Jesús Llorente (UCM), Carlos Mora Corral (UAM), José Manuel Rodríguez (UC3M) y Juan B. Seoane (UCM).
Fecha: 25 al 27 de septiembre de 2023
Lugar: Aula Miguel de Guzmán y Salón de Actos
Colaboran: Universidad Complutense de Madrid (UCM), Instituto de Matemática Interdisciplinar (IMI), Universidad Carlos III de Madrid (UC3M) y Universidad Autónoma de Madrid (UAM).
VI Concurso de Modelización Matemática del IMI (CMM-IMI 2023)
Días: Del 28 de septiembre al 2 de octubre de 2023
Días: Del 28 de septiembre al 2 de octubre de 2023
Más información: https://blogs.mat.ucm.es/cmm/
Seminario de Análisis Matemático y Matemática Aplicada
Título: Ecuaciones de Hamilton-Jacobi difusivas y sus singularidades
Orador: Philippe Souplet (Université de la Sorbonne, Paris Nord)
J. López-Gómez, E. Muñoz-Hernández, F. Zanolin, Subharmonic solutions for a class of predator-prey models with degenerate weights in periodic environments. Open Mathematics, 21(1), 2023. http://dx.doi.org/10.1515/math-2022-0593
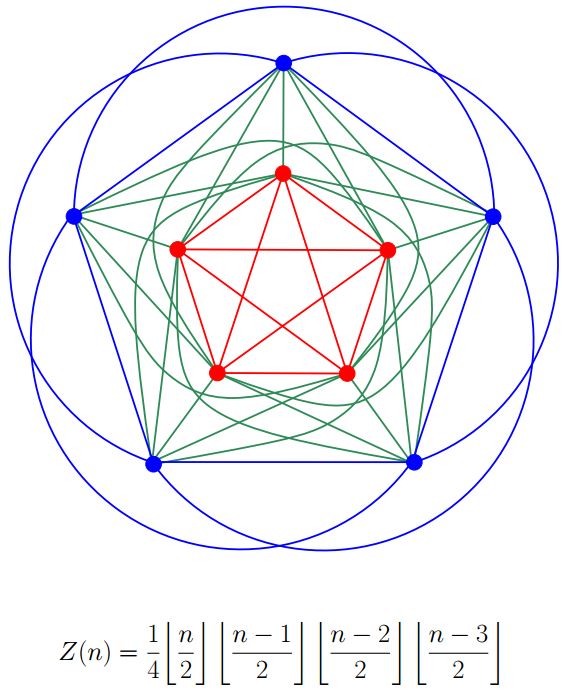
Un grafo G=(V,E) es una colección de vértices V y de pares de vértices E (las aristas) y un dibujo de un grafo es una representación en el plano de esta estructura. Los grafos son objetos fundamentales de la Matemática Discreta y permiten modelar multitud de situaciones.
El número de cruce de un grafo se define como el menor número de cruces posible en cualquier dibujo de un grafo, y calcularlo es un problema de dificultad notable, que además de su belleza matemática tiene aplicaciones, por ejemplo, en el diseño de circuitos integrados.
Kn denota al grafo completo de n vértices (las aristas son todos los pares de vértices) y el problema de determinar su número de cruce sigue desafiando los ataques de los últimos 60 años.
En la imagen se puede ver un dibujo de K10 con 60 cruces (el mínimo posible).
[2] Shengjun Pan y R. Bruce Richter. The crossing number of K11 is 100. Journal of Graph Theory, 56(2), 128–134 (2007).
[3] Oswin Aichholzer. Another small but long step for crossing numers: cr(13)=225 and cr(14)=315. Proceedings of the Canadian Conference on Computational Geometry (2021).
[4] Bernardo Ábrego, Oswin Aichholzer, Silvia Fernández-Merchant, Pedro Ramos y Gelasio Salazar: Shellable drawings and the cylindrical crossing number of Kn . Discrete & Computational Geometry, 52 (4), 743-753 (2014).
Fecha: 28 de septiembre, 2023
Lugar: Aula B07
Hora: 13:00
Organizado por: Departamento de Análisis Matemático y Matemática Aplicada e Instituto de Matemática Interdisciplinar (IMI)
J. Ferrer, D. García, M. Maestre, G. A. Muñoz, D. L. Rodríguez, J. B. Seoane. Geometry of the Unit Sphere in Polynomial Spaces. Springer. 2023. ISBN: 978-3-031-23675-4
J. López-Gómez, E. Muñoz-Hernández, F. Zanolin, Subharmonic solutions for a class of predator-prey models with degenerate weights in periodic environments. Open Mathematics, 21(1), 2023. http://dx.doi.org/10.1515/math-2022-0593
Seminario de Análisis Matemático y Matemática Aplicada
Title: A method for solving the Cauchy problema in cardiac electrophysiology. Generalization to solving unstable forecast problems
Speaker: Jaques Henry (INRIA Bordeaux)
Day: October 2, 2023
Place: Room B07
Hour: 13:00
Organized by: Departamento de Análisis Matemático y Matemática Aplicada and Instituto de Matemática Interdisciplinar (IMI)
Seminario de Análisis Matemático y Matemática Aplicada
Title: Some mathematical models of the mechanical and electrical activity of the heart: forward and inverse problems
Speaker: Andrés Fraguela Collar (Autonomous University of Puebla, Mexico)
Day: October 3, 2023
Place: Aula B07
Hora: 13:00
Organized by: Departamento de Análisis Matemático y Matemática Aplicada and Instituto de Matemática Interdisciplinar (IMI)
5) 1+400. Divulgación con 1 imagen y 400 palabras
Pedro Ramos Alonso. ¿Cuál es la mejor forma de conectar n puntos del plano?
Boletín del IMI, Nº 101 (21 septiembre 2023), Sección "1+400. Divulgación con 1 imagen y 400 palabras."
________________________________________________________________
En esta sección se publican artículos cortos de divulgación, con una imagen y un máximo de 400 palabras (sin tener en cuenta en estas restricciones los datos de los autores). Las personas que quieran publicar un artículo pueden enviarlo a secreadm.imi@mat.ucm.es
La colección de todos los artículos publicados en esta sección se puede ver en www.ucm.es/imi/1mas400
Pedro Ramos Alonso es profesor titular de universidad en el departamento de física y matemáticas de la Universidad de Alcalá. Su carrera investigadora se desarrolla fundamentalmente en el área de la Geometría Discreta y Computacional, y en el último decenio su interés se ha trasladado al área de la educación matemática centrándose, en particular, en la formación matemática (inicial y continua) de docentes, tanto de primaria como de secundaria.
_________________________________________________________________
¿Cuál es la mejor forma de conectar n puntos del plano?
Pedro Ramos AlonsoSupongamos que queremos conectar n puntos del plano (todos entre sí) y que queremos hacerlo sin que se produzcan intersecciones entre las conexiones. Es muy sencillo comprobar que si las conexiones pueden ser curvas simples, e independientemente de la posición de los puntos, siempre se puede hacer si n=4 y no es complicado convencerse de que la tarea se vuelve imposible si n=5. En el lenguaje de la Teoría de Grafos, decimos que el grafo completo de 5 vértices no es plano.
Un grafo G=(V,E) es una colección de vértices V y de pares de vértices E (las aristas) y un dibujo de un grafo es una representación en el plano de esta estructura. Los grafos son objetos fundamentales de la Matemática Discreta y permiten modelar multitud de situaciones.
El número de cruce de un grafo se define como el menor número de cruces posible en cualquier dibujo de un grafo, y calcularlo es un problema de dificultad notable, que además de su belleza matemática tiene aplicaciones, por ejemplo, en el diseño de circuitos integrados.
Kn denota al grafo completo de n vértices (las aristas son todos los pares de vértices) y el problema de determinar su número de cruce sigue desafiando los ataques de los últimos 60 años.
En la imagen se puede ver un dibujo de K10 con 60 cruces (el mínimo posible).
Este dibujo, que puede encontrarse en [1] y puede generalizarse fácilmente para n vértices, se conoce como dibujo cilíndrico, porque se puede pensar que los vértices se sitúan en un cilindro finito (como una lata de refresco). Se sitúan la mitad de los vértices en la circunferencia de cada tapa y se conectan con la curva más corta. El número de cruces en este caso viene dado por la expresión Z(n) (ver imagen) y se conjetura que es el óptimo. No se conoce ningún dibujo de Kn con menos de Z(n) cruces, aunque solo se ha podido demostrar que Z(n) es, de hecho, el número de cruce de Kn para n≤14 [2,3]. Para el caso general de n vértices, el resultado más reciente sobre este problema se debe a Ábrego et al. [4], que demostraron que la cota es óptima para cierto tipo de dibujos. La demostración es “elemental”, en el sentido de que no usa ningún aparato matemático que no conozca un estudiante de 1º de Grado.
[1] Frank Harary, Andrew Hill: On the number of crossings in a complete graph. Proc. Edinb. Math. Soc. 13, 333–338 (1963).
[2] Shengjun Pan y R. Bruce Richter. The crossing number of K11 is 100. Journal of Graph Theory, 56(2), 128–134 (2007).
[3] Oswin Aichholzer. Another small but long step for crossing numers: cr(13)=225 and cr(14)=315. Proceedings of the Canadian Conference on Computational Geometry (2021).
[4] Bernardo Ábrego, Oswin Aichholzer, Silvia Fernández-Merchant, Pedro Ramos y Gelasio Salazar: Shellable drawings and the cylindrical crossing number of Kn . Discrete & Computational Geometry, 52 (4), 743-753 (2014).
Comic strip sent by Christopher J. Burke and used with permission.
7) Math Puzzle
Solution to last week's Math Puzzle, sent by Kjartan Poskitt and published on issue No. 101 of the Boletín del IMI:
| Instituto de Matemática Interdisciplinar Universidad Complutense de Madrid Plaza de Ciencias 3, 28040, Madrid https://www.ucm.es/imi Haga click aquí para recibir el Boletín del IMI / Click here to receive the Boletín del IMI Para dejar de recibir el Boletín del IMI escriba a secreadm.imi@mat.ucm.es / To unsubscribe send an email to secreadm.imi@mat.ucm.es Los anteriores boletines se pueden encontrar en / Previous bulletins can be found at https://www.ucm.es/imi/boletin-del-imi |