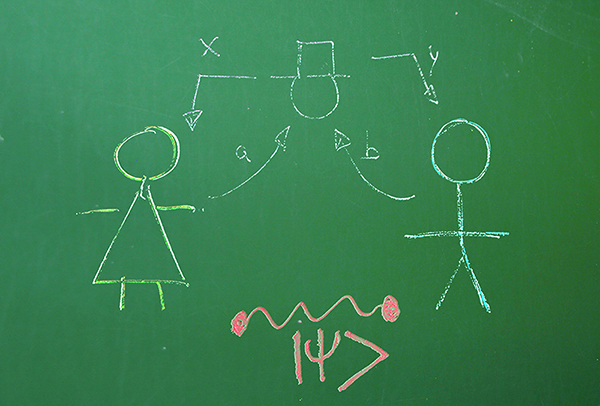Main research lines
Bell inequalities and quantum non-locality
Bell"s inequalities date back to the famous work of Einsten, Podolsky and Rosen in 1935, where the authors raise an apparent dilemma about the completeness of quantum mechanics as a model for Nature. 30 years later, Bell proposed an ideal experiment to test that quantum mechanics is in fact not compatible with a classical explanation of Nature in terms of hidden variables. After a series of experiments initiated by A. Aspect and co-authors in the 70"s, in 2015 the definitive experiment that separates quantum physics from the classical one was obtained in Delft, obtaining the desired violations of Bell"s inequalities. At the practical level, violations of Bell"s inequalities are behind some of the most important applications of quantum information, such as quantum cryptography and the secure generation of random numbers, both already in a commercial phase.
On the other hand, Bell"s inequalities are closely related to Interactive Proof Systems (IPS). IPS play a central role in complexity theory since the famous PCP Theorem, which allowed to prove among other things that many problems on graphs (such us finding the largest complete subgraph) are difficult to approximate to any reasonable precision, unless P = NP. IPS are also the model for studying the so-called communication complexity, which is a central problem in parallel computing.
The work on the group focuses on the use of advanced tools from mathematical analysis (operator spaces, local Banach space theory, random matrix theory) to produce significant advances in the understanding of Bell inequalities and their applications.
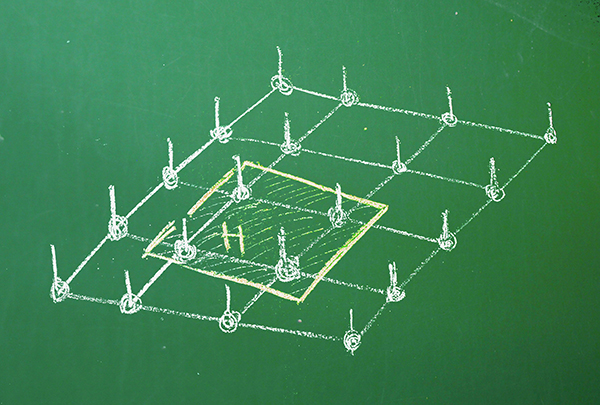The classification of quantum phases of matter
When talking about different phases in Physics, the first thing that comes to mind is the division in solid, liquid and gas, where temperature is the varying parameter which connects them through phase transition points. At zero (or close to zero) temperature, where quantum mechanics is the physical law that governs the system, there are also different phases interconnected via phase transitions. The exotic and unexpected properties of some of these quantum phases, like superconductivity, superfluidity, fractional statistics, topological order, etc. have attracted the attention of physicists for many years.
The main aim of this research line is to catalogue, in a mathematically rigorous way, the possible global properties that may be present in a material at very low temperature and provide models that possess each one of them. In this way we would have a kind of periodic table of the quantum phases of matter.
In order to do that, we need to deal with the mathematical problem of characterizing the existence or absence of a spectral gap in the operator (called the Hamiltonian) that models the interactions of a system and governs its evolution. The spectral gap represents the energy the system needs to change its properties. One can then formalize the definition of phases as regions in parameter space where the spectral gap is positive, and phase transitions as points where the spectral gap vanishes. This guarantees that systems within the same phase have similar properties and phase transitions are unstable points where properties change abruptly.